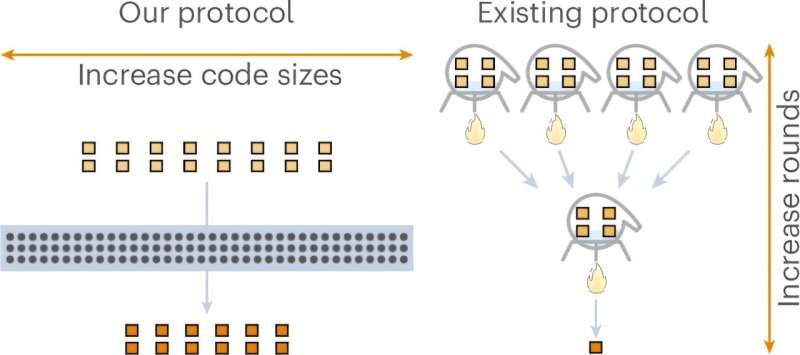
Researchers have successfully demonstrated that the optimal scaling for magic state distillation, a crucial process in achieving fault-tolerant quantum computing, is now attainable for qubits. This advancement, published in Nature Physics, marks a significant improvement over previous results, achieving a scaling exponent of exactly zero. This breakthrough addresses a long-standing challenge in the quantum computing field.
The study’s lead author, Adam Wills, a Ph.D. student at MIT’s Center for Theoretical Physics, emphasized the importance of this achievement. He explained that while building quantum computers is an inspiring goal, the persistent issue of noise poses a significant barrier. Qubits, the fundamental units of quantum information, are highly sensitive to their environments, necessitating robust error-correcting codes to preserve their integrity.
Error correction alone cannot overcome all challenges. The codes currently in use primarily support operations known as Clifford gates, which do not deliver the full advantages of quantum computing on their own. Implementing necessary non-Clifford operations in a fault-tolerant manner has remained a significant hurdle. The concept of magic state distillation, introduced by Bravyi and Kitaev in 2005, allows these operations to be performed through specially prepared quantum states. However, the process has been resource-intensive, with the overhead—the ratio of noisy input states required to produce a high-quality output state—growing as error rates decrease.
The Role of Magic States in Quantum Computing
Magic states are a quantifiable resource in quantum computing. To achieve universal quantum computation, Clifford operations must be supplemented with these special states. Magic states lie outside the realm of stabilizer states, which correspond to classical computational capabilities. They possess quantum contextuality, providing quantum computers with their unique advantages over classical systems.
To execute necessary non-Clifford gates, such as the T gate, quantum computers consume magic states through a process called gate teleportation. Currently, researchers produce noisy magic states with error rates around 10^-3. For quantum advantage, these rates must decrease to about 10^-7, and for large-scale algorithms, goals as low as 10^-15 are essential. This is where the optimization of magic state distillation becomes critical.
Achieving constant overhead in the distillation process is a measure of its efficiency. For many years, as the target error rate decreased, the overhead required increased, characterized by a scaling exponent known as gamma (γ). A lower γ indicates greater efficiency in the distillation process. With the recent findings, achieving γ = 0 means constant overhead regardless of the quality of the final states.
Previous advancements in the field include work by Hastings and Haah, who reached γ ≈ 0.678 in 2017. In 2018, Krishna and Tillich approached γ = 0 but only for increasingly large quantum systems with no clear pathway to practical applications. Wills and his team demonstrated that achieving γ = 0 is indeed possible.
Innovative Discoveries in Distillation Techniques
Wills noted that their discovery unfolded in two key stages. Initially, they recognized the potential of algebraic geometry codes for addressing the challenge. Earlier attempts utilized different classical error-correcting codes, such as Reed-Muller and Reed-Solomon codes, but fell short of achieving constant overhead scalability.
Algebraic geometry codes, which have strong error-correction properties, were able to maintain constant overhead for 1024-dimensional qudits, a more complex quantum system than the two-level qubits typically employed in practical quantum computing. The second stage of their discovery involved insights from a textbook by Dan Gottesman. By exploring a lesser-known chapter, the researchers realized they could represent their qudits as sets of qubits, allowing them to adapt their protocol for qubits with only a minimal overhead loss.
As a result of these innovations, the team established that constant overhead (γ = 0) is achievable for qubit systems, presenting a significant theoretical limit for future research.
Despite the promising theoretical implications, Wills cautioned about the gap between theory and practical implementation. The theoretical scaling of γ = 0 may not directly translate to current quantum computing capabilities, as the resource requirements could exceed what is available in contemporary quantum systems. Nevertheless, laying down a solid theoretical foundation is vital for advancing fault-tolerant quantum computing.
Wills remarked, “Developing a solid theory of quantum magic is incredibly important for pushing fault-tolerance further in all regimes, because we know it is essential for universal quantum computation.” He noted that subsequent studies are likely to build on their findings, focusing on adapting these theoretical concepts for near-term applications.
The team is already exploring new directions, including optimizing constant factors, investigating quantum low-density parity-check (LDPC) code variants, and determining the best methods for converting qudits to qubits.
This research was carefully reviewed and published, underscoring the importance of credible, peer-reviewed work in the field of quantum computing. As advancements continue, the implications for technology and computation remain profound, paving the way for more resilient and capable quantum systems in the future.